Image Classification Tutorial

Introduction
We will carry out a supervised classification using Sentinel-2 data for the Gewata region in Ethiopia. Atmospherically corrected Level 2A data acquired on December 27 2020 is used in this exercise. The data is downloaded from ESA’s online data hub (https://scihub.copernicus.eu/dhus), a part of the Copernicus European Programme. As it is freely available, Sentinel data has been commonly used next to Landsat data for environmental monitoring.
Data Download
Download the data to your computer and open your preferred R IDE (R Studio) to the directory of this tutorial.
After downloading the data we will first visualize it. The data consists of all the Sentinel-2 bands at a spatial resolution of 20 m. We will also make use of training polygons for the land cover classification. We will be making use of the RasterBrick object.
Set up & Data Exploration
After downloading and unzipping the data folder open it and make sure it has an renv.lock file, then open the ImageClassificationTutorial.rmd file in RStudio . The first step will be to download all the necessary packages needed to run the code this will be done using renv, by writing the following code in the console and typing ‘y’ when asked “Would you like to restore this project from the.lock file?”
renv::restore()
We will be loading packages as we get to using them in the code.
library(raster)
library(sf)
## Change the data_dir (directory) to the folder where you downloaded your data, if you opened the ImageClassificationTutorial.rmd file this should automatically be done for you.
## data_dir<-"C:/Data/M4L/Core_IC/"
Gewata<-brick(file.path(data_dir, "S2B2A_T36NZP_20201227T075239_20m_gewata_crop.tif"))
names(Gewata)<-readLines(file.path(data_dir, "S2B2A_T36NZP_20201227T075239_20m_gewata_bands.txt"))
Visualize the data and explore some attributes
# The image is cloud-free, so drop the cloud mask layer
Gewata<-dropLayer(Gewata, "SCL")
## Check out the attributes
Gewata$B02
## Some basic statistics using cellStats() from the raster package
cellStats(Gewata$B02, stat=max)
cellStats(Gewata$B02, stat=mean)
# This is equivalent to:
maxValue(Gewata$B02)
## What is the maximum value of all three bands?
max(c(maxValue(Gewata$B02), maxValue(Gewata$B8A), maxValue(Gewata$B11)))
## summary() is useful function for a quick overview
summary(Gewata$B02)
You might get different values for cellStats an maxValue, the reason for this is that the cellStats looks at all the pixel values, whereas the maxValue function takes a subset of the pixel values. As a result maxValue is faster than cellStats.
# histograms for all the bands in one window (automatic, if a RasterBrick is supplied)
hist(Gewata, maxpixels=1000)
Note that the values of these bands have been rescaled by a factor of 10,000. This is done for file storage considerations. For example, a value of 0.5643 stored as a float takes up more disk space than a value of 5643 stored as an integer. If you prefer reflectance values in their original scale (from 0 to 1), this can easily be done using raster algebra or calc().
A scatter plot matrix can be helpful in exploring relationships between raster layers. This can be done with the pairs() function of the raster package, which (like hist()) is a wrapper for the same function found in the graphics packages. R Source
pairs(Gewata, maxpixels=1000)
Note that both hist() and pairs() compute histograms and scatter plots based on a random sample of raster pixels. The size of this sample can be changed with the argument maxpixels in either function.
Calling pairs() on a RasterBrick reveals potential correlations between the layers themselves. In the case of bands of the Gewata subset, we can see that band 3 and 5 (in the visual part of the Electro-Magnetic, EM spectrum) and bands 6 and 7 (in the near infrared part of the EM spectrum) are highly correlated. Similar correlation also exist between band 11 and 12. While band 8a contains significant non-redundant information.
Question 1
Given what we know about the location of these bands along the EM spectrum, how could these scatterplots be explained?
A commonly used metric for assessing vegetation dynamics, the normalized difference vegetation index (NDVI), can be calculated to use as another variable for the classification. NDVI can be calculated using direct raster algebra, calc() or overlay(). Since we will be using NDVI again later in this tutorial, let’s calculate it and store it in our workspace using overlay().
par(mfrow = c(1, 1)) # reset plotting window
ndvi <- overlay(Gewata$B8A, Gewata$B04, fun=function(x,y){(x-y)/(x+y)})
plot(ndvi)
Aside from the advantages of calc() and overlay() regarding memory usage, an additional advantage of these functions is the fact that the result can be written immediately to the file by including the filename = "..." argument, which will allow you to write your results to file immediately, after which you can reload in subsequent sessions without having to repeat your analysis.
Question 2
What is the advantage of including NDVI layer in the classification?
Classifying raster data
One of the most important tasks in analysis of remote sensing image analysis is image classification. In classifying the image, we take the information contained in the various bands (possibly including other synthetic bands such as NDVI or principal components). There are two approaches for image classification: supervised and unsupervised. In this tutorial we will explore supervised classification based on the Random Forest method.
Random Forest classification
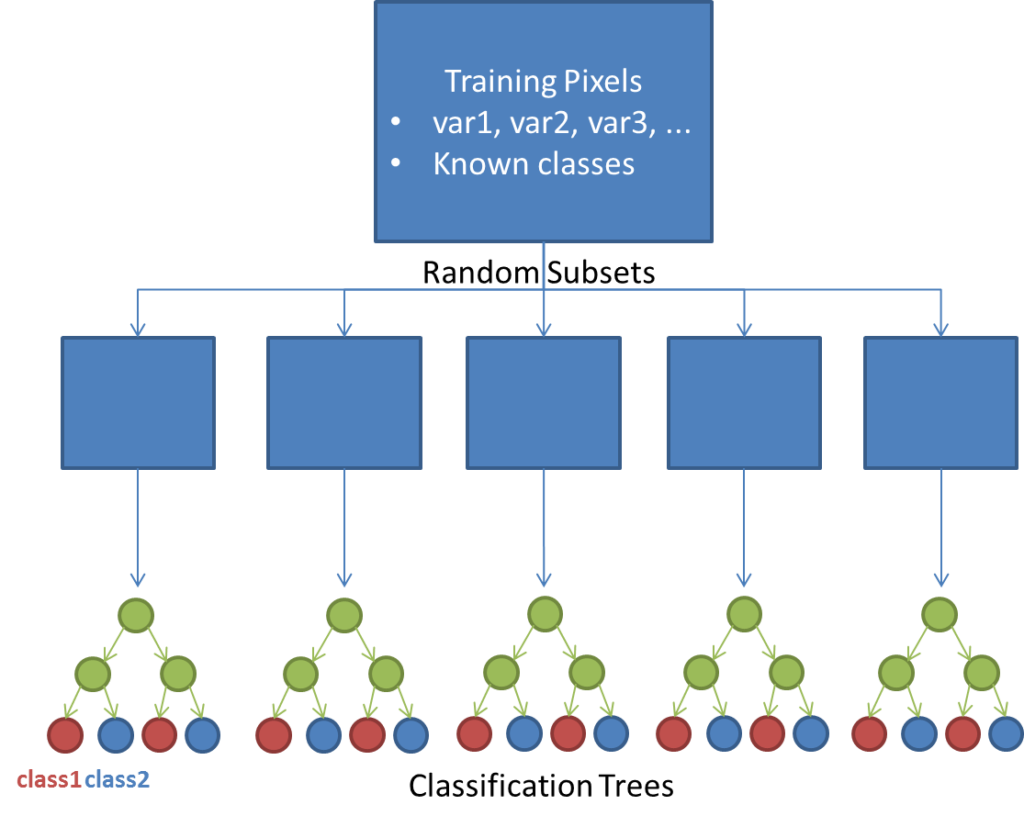
The Random Forest classification algorithm is an ensemble learning method that is used for both classification and regression. In our case, we will use the method for classification purposes. Here, the Random Forest method takes random subsets from a training dataset and constructs classification trees using each of these subsets. Trees consist of branches and leaves.
Branches represent nodes of the decision trees, which are often thresholds defined for the measured (known) variables in the dataset. Leaves are the class labels assigned at the termini of the trees. Sampling many subsets at random will result in many trees being built. Classes are then assigned based on classes assigned by all of these trees based on a majority rule, as if each class assigned by a decision tree were considered to be a vote.
The figure below gives a simple demonstration of how the random forest method works in principle. For an introduction to the Random Forest algorithm, see this presentation. For more information on random forest implementation in R see this tutorial.
One major advantage of the Random Forest method is the fact that an Out Of the Bag (OOB) – cross validation error estimate and an estimate of variable performance are performed. For each classification tree assembled, a fraction of the training data are left out and used to compute the error for each tree by predicting the class associated with that value and comparing with the already known class. This process results in a confusion matrix, which we will explore in our analysis. In addition, an importance score is computed for each variable in two forms: the mean decrease in accuracy for each variable, and the Gini impurity criterion, which will also be explored in our analysis.
To perform the classification in R, it is best to assemble all covariate layers (ie. those layers containing predictor variable values) into one RasterBrick object. In this case, we can simply append the new layer (NDVI) to our existing RasterBrick (currently consisting of different bands).
First, let’s rescale the original reflectance values to their original scale. This step is not required for the RF classification, but it might help with the interpretation, if you are used to thinking of reflectance as a value between 0 and 1. (On the other hand, for very large raster bricks, it might be preferable to leave them in their integer scale, but we won’t go into more detail about that here.)
gewata <- calc(Gewata, fun=function(x) x / 10000)
## Make a new RasterStack of covariates by 'stacking' together the existing gewata brick and NDVI
covs <- stack(gewata, ndvi)
plot(covs)
You’ll notice that we didn’t give our NDVI layer a name yet. It’s good to make sure that the raster layer names make sense, so you don’t forget which band is which later on. Let’s change all the layer names (make sure you get the order right!).
names(covs) <- c(names(Gewata),"NDVI")
names(covs)
Training data preparation
For this exercise, we will do a very simple classification for 2020 using three classes: forest, cropland and wetland. While for other purposes it is usually better to define more classes (and possibly fuse classes later), a simple classification like this one could be useful, for example, to construct a forest mask for the year 2020
## we load the training polygons as a csv file using st_read:
trainingPoly <- st_read("data/trainingPoly.csv")
## Superimpose training polygons onto NDVI plot
par(mfrow = c(1, 1)) # reset plotting window
plot(ndvi)
plot(trainingPoly, add = TRUE)
The training classes are labelled as string labels. For this exercise, we will need to work with integer classes, so we will need to first ‘relabel’ our training classes. There are several approaches that could be used to convert these classes to integer codes. In this case, we will first make a function that will reclassify the character strings representing land cover classes into integers based on the existing factor levels.
## Inspect the trainingPoly object
trainingPoly<-trainingPoly[,c(2:4)] #remove an unused column
trainingPoly
# The 'Class' column is a character but should be converted to factor
summary(trainingPoly$Class)
trainingPoly$Class <- as.factor(trainingPoly$Class)
summary(trainingPoly$Class)
# We can make a new 'Code' column by converting the factor levels to integer by using the as.numeric() function,
trainingPoly$Code <- as.numeric(trainingPoly$Class)
# Inspect the new 'Code' column
summary(trainingPoly$Code)
## Plotting
# Define a colour scale for the classes (as above)
# corresponding to: cropland, forest, wetland
cols <- c("orange", "dark green", "light blue")
### Superimpose training polygons (colour by class) onto NDVI plot
plot(ndvi)
plot(trainingPoly["Class"], add = TRUE, pal=cols)
## Add a customised legend
legend("topright", legend=c("cropland", "forest", "wetland"), fill=cols, bg="white")
Our goal in preprocessing this data is to have a table of values representing all layers (covariates) with known values/classes. To do this, we will first need to know the values of the covariates at our training polygon locations. We can use extract function of raster package for this. Next we convert these data to a data.frame representing all training data.
## Extract pixel values below the polygons
trainingData<-extract(covs, trainingPoly)
# Check structure
str(trainingData)
# It is a matrix (rows are pixels, columns are bands) per polygon
# Convert each matrix to a data.frame and add the class column from the polygons
valuetable <- lapply(1:length(trainingData), function(polygonID) cbind.data.frame(trainingData[[polygonID]], Class=trainingPoly$Class[polygonID]))
# Unlist into one long data.frame
valuetable <- do.call(rbind, valuetable)
This data frame will be used as an input into the RandomForest classification function. We then inspect the first and last 10 rows.
head(valuetable, n = 10)
tail(valuetable, n = 10)
We have our training dataset as a data.frame with the class column as a factor. If it is integer, random forest regression will be run, instead of classification. So, good to check on that.
Now we have a convenient training data table which contains, for each of the three defined classes, values for all covariates. Let’s visualize the distribution of some of these covariates for each class. To make this easier, we will create 3 different data.frames for each of the classes. This is just for plotting purposes, and we will not use these in the actual classification.
val_crop <- subset(valuetable, Class == "cropland")
val_forest <- subset(valuetable, Class == "forest")
val_wetland <- subset(valuetable, Class == "wetland")
## NDVI
par(mfrow = c(3, 1))
hist(val_crop$NDVI, main = "cropland", xlab = "NDVI", xlim = c(0, 1), col = "orange")
hist(val_forest$NDVI, main = "forest", xlab = "NDVI", xlim = c(0, 1), col = "dark green")
hist(val_wetland$NDVI, main = "wetland", xlab = "NDVI", xlim = c(0, 1), col = "light blue")
par(mfrow = c(1, 1))
Other covariates, such as the other bands can also be plotted like above.
## 3. Bands 8a and 11 (scatterplots)
plot(B8A ~ B11, data = val_crop, pch = ".", col = "orange", xlim = c(0, 0.4), ylim = c(0, 0.5))
points(B8A ~ B11, data = val_forest, pch = ".", col = "dark green")
points(B8A ~ B11, data = val_wetland, pch = ".", col = "light blue")
legend("topright", legend=c("cropland", "forest", "wetland"), fill=c("orange", "dark green", "light blue"), bg="white")
Question 3
Try to produce the same scatter plot plot as above looking at the relationship between other bands. Try B02 & B05, B07 & NDVI (you might have adjusted the xlim to incorporate the NDVI values) and another of your choice. What can you say about the relationships between these bands? Which ones give a clear distinction between classes, and where is this less clear?
We can see from these distributions that these covariates may do well in classifying forest pixels, but we may expect some confusion between cropland and wetland (although the individual bands may help to separate these classes). You can save the training data using the write.csv() command, in case something goes wrong after this point, and you need to start over again.
Run Random Forest Classification
We build the Random Forest model using the training data. For this, we will use the ranger package in R. There is also randomForest package available in R. However, ranger is implemented in C++ with multithreading and thus is much faster. Using the ranger() function, we will build a model based on a matrix of predictors or covariates (ie. the first 10 columns of valuetable) related to the response (the Class column of valuetable).
Construct a random forest model
Covariates (x) are found in columns 1 to 10 of valuetable. Training classes (y) are found in the ‘class’ column of valuetable. Caution: this step takes fairly long! but can be shortened by setting importance=FALSE
library(ranger)
modelRF <- ranger(x=valuetable[, 1:ncol(valuetable)-1], y=valuetable$Class,
importance = "permutation", seed=0xfedbeef)
Since the random forest method involves the building and testing of many classification trees (the ‘forest’), it is a computationally expensive step (and could take a lot of memory for especially large training datasets). When this step is finished, it would be a good idea to save the resulting object with the saveRDS() command. Any R object can be saved as an .rds file and reloaded into future sessions using readRDS().
Note: there is a similar functionality using the save() and load() commands, but those can save more than one object and don’t tell you their names, you have to know them. That is why saveRDS()/readRDS() is preferred, but in this tutorial in a lot of cases load is still being used.
The resulting object from the ranger() function is a specialized object of class ranger, which is a large list-type object packed full of information about the model output. Elements of this object can be called and inspected like any list object.
## Inspect the structure and element names of the resulting model
modelRF
class(modelRF)
#str(modelRF)
names(modelRF)
## Inspect the confusion matrix of the OOB error assessment
modelRF$confusion.matrix
Earlier we provided a brief explanation of OOB error, though it can be a valuable metric for evaluating your model, it can overestimate the true prediction error depending on the parameters presents in the model.
Since we set importance="permutation", we now also have information on the statistical importance of each of our covariates which we can retrieve using the importance() command.
importance(modelRF)
The above shows the variable importance for a Random Forest model, showing the mean decrease in accuracy for each variable.
The mean decrease in accuracy indicates the amount by which the classification accuracy decreased based on the OOB assessment. In this case, it seems that Gewata bands 12 and 2 have the highest impact on accuracy. For large datasets, it may be helpful to know this information, and leave out less important variables for subsequent runs of the ranger() function.
Since the NDVI layer scores relatively low according to the mean accuracy decrease criterion, try to construct an alternate Random Forest model as above, but excluding this layer, you can name it something like ‘modelRF2’.
Question 4
What effect does this have on the overall accuracy of the results (hint: compare the confusion matrices of the original and new outputs). What effect does leaving this variable out have on the processing time (hint: use system.time())?
Now we apply this model to the rest of the image and assign classes to all pixels. Note that for this step, the names of the raster layers in the input brick (here covs) must correspond exactly to the column names of the training table. We will use the predict() function from the raster package. This function uses a pre-defined model to predict values of raster cells based on other raster layers. This model can be derived by a linear regression, for example. In our case, we will use the model provided by the ranger() function.
## Double-check layer and column names to make sure they match
names(covs)
names(valuetable)
## Predict land cover using the RF model
predLC <-raster::predict(covs, modelRF, fun=function(...) predict(...)$predictions)
## Plot the results
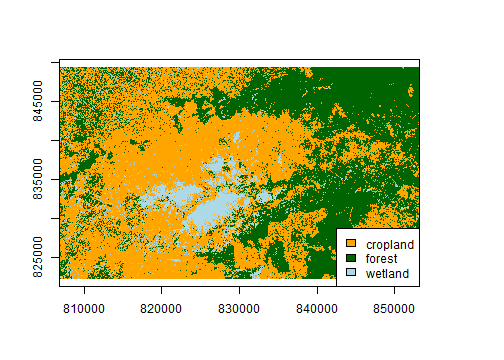
# recall: 1 = cropland, 2 = forest, 3 = wetland
cols <- c("orange", "dark green", "light blue")
plot(predLC, col=cols, legend=FALSE)
legend("bottomright",
legend=c("cropland", "forest", "wetland"),
fill=cols, bg="white")
Note that the predict() function also takes arguments that can be passed to writeRaster() (eg. filename = "", so it is a good idea to write to file as you perform this step (rather than keeping all output in memory).
Assessing the accuracy of the classification
Previously, we have seen the classification accuracy based on the OOB error within the ModelRF object. As those accuracy metrics are based on the training data itself, it is important to assess the classifcation using a separate validation dataset. Here use a validation dataset to assess the classification quality. Generally, you can select random sample locations based on the classified map and collect the validation data.
## we load the validation data :
validationPoints<-readRDS("data/validation")
names(validationPoints)<-c("x","y","refLC")
#extract the value of land cover map on the validation locations
validationPoints$mapLC<-extract(predLC, validationPoints)
head(validationPoints)
#remove NA values
validationPoints<-validationPoints[!is.na(validationPoints$mapLC),]
dim(validationPoints)
Once we have the mapped and reference land cover types in the same data frame, we can create the confusion matrix (also referred to as error matrix) to calculate the map accuracy.
#confusion matrix
cm<-table(validationPoints$mapLC, validationPoints$refLC)
row.names(cm)<-c("cropland", "forest", "wetland")
colnames(cm)<-c("cropland", "forest", "wetland")
print(cm)
#calculate overall accuracy
o.a<-sum(diag(cm))/sum(cm)*100
print(paste0("Overall accuracy: ", round(o.a,1)))
#user's accuracy
user.ac<-diag(cm)/rowSums(cm)*100
print("User's accuracy")
print(round(user.ac,1))
#producer's acc
producer.ac<-diag(cm)/colSums(cm)*100
print("Producer's accuracy")
print(round(producer.ac,1))
Question 5
Where is most of the error coming from in the classification. (Hint: It may also be helpful to look back at the plots in the first part of the tutorial). How can our classification be further improved?
Overall accuracy based on validation data is about 70.0%. It is as expected to be lower than the OOB as a separate validation data is used.